公约数和公倍数
参看:
1.质数和合数
质数是指在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数。 合数是指在大于 1 的整数中除了能被 1 和本身整除外,还能被其他数(0 除外)整除的数。与之相对的是质数,而 1 既不属于质数也不属于合数。最小的合数是 4。
2.公约数
概念:多个整数共有约数中最大的一个(16 和 12 的最大公约数为 4),a,b 的最大公约数记为(a,b),同样的,a,b,c 的最大公约数记为(a,b,c),多个整数的最大公约数也有同样的记号。

求最大公约数有多种方法,常见的有质因数分解法、短除法、辗转相除法、更相减损法。
2.1 质因数分解法求公约数
把一个合数分解成若干个质因数的乘积的形式,即求质因数的过程叫做分解质因数。分解质因数只针对合数。
/**
* 列出小于等于某个数的全部质数
* @param {number} maxValue | 30
* @return {number[]} primes | [2,3,5, ...]
*/
function prime(maxValue) {
let minPrime = 2;
let primes = [minPrime];
// 遍历所有数
for (let i = 3; i <= maxValue; i++) {
let isPrime = true;
// 将遍历的数依次在找到的质数数组每一项取余,没有余数说明这个数不是质数,break本次循环,然后判断下一个数
for (let p = 0; p < primes.length; p++) {
if (i % primes[p] == 0) {
isPrime = false;
break;
}
}
if (isPrime) {
primes.push(i);
}
}
return primes;
}
/**
* 找出这个数的所有公约数
* @param {number} v | 18
* @return {number} results | [2, 3, 3 ]
*/
function decomposition(v) {
let results = [];
let primes = prime(v);
console.log(primes);
let tmp = v;
for (let i = 0; i < primes.length; i++) {
// 判断这个数是否等于 遍历的质数,是则终止循环
if (tmp == primes[i]) {
results.push(primes[i]);
break;
}
// 这个数循环除以某个质数,将这个数中的相同质数取尽,然后将商重新赋值给 tmp,接着遍历下一个质数
while (tmp % primes[i] == 0) {
tmp /= primes[i];
results.push(primes[i]);
}
}
// 如果这个数的质因数数组长度为1,那么,这个数只有1和它本身2个质因数
if (results.length == 1) {
results = [];
results.push(1);
results.push(v);
}
return results;
}
console.log(decomposition(7));
3.最大公约数
3.1 短除法
求几个数最大公因数的方法,开始时用观察比较的方法,即:先把每个数的因数找出来,然后再找出公因数,最后在公因数中找出最大公因数。
3.2 辗转相除法
/**
* @method gcd | 最大公约数
* @param { Number } a | 40
* @param { Number } b | 104
* @return { Number } a和b的最大公约数 | 8
*/
const gcd = (a, b) => {
// 利用es6数组解构方法巧妙地置换a和b的值,目的使a大于b
if (a < b) [a, b] = [b, a];
// 0 和 任何数的最大公约数都是这个数
if (b === 0) return a;
// 递归将除数和余数继续执行
if (a % b !== 0) return gcd(b, a % b);
// 返回最大公约数
else return b;
};
// 调用
console.log(gcd(104, 40)); // 8
console.log(gcd(40, 104)); // 8
console.log(gcd(0, 40)); // 8
3.3 更相减损法
- 第一步:任意给定两个正整数;判断它们是否都是偶数。若是,则用 2 约简;若不是则执行第二步。
- 第二步:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。 -则第一步中约掉的若干个 2 的积与第二步中等数的乘积就是所求的最大公约数。
/**
* @method gcd | 最大公约数
* @param { Number } a | 40
* @param { Number } b | 104
* @return { Number } a和b的最大公约数 | 8
*/
function gcd(num1, num2) {
if (num1 < num2) [num1, num2] = [num2, num1];
if (num1 * num2 === 0) return num2;
let minPrime = 1;
while (num1 % 2 == 0 && num2 % 2 == 0) {
num1 = num1 / 2;
num2 = num2 / 2;
minPrime *= 2;
}
let cha = num1 - num2;
while (cha !== num2) {
if (cha - num2 > 0) {
num1 = cha;
} else {
num1 = num2;
num2 = cha;
}
cha = num1 - num2;
}
return minPrime == 1 ? cha : cha * minPrime;
}
// 调用
console.log(gcd(104, 40)); // 8
console.log(gcd(40, 104)); // 8
console.log(gcd(0, 40)); // 8
4.最小公倍数
两个或多个整数公有的倍数叫做它们的公倍数,其中除 0 以外最小的一个公倍数就叫做这几个整数的最小公倍数。
4.1 分解质因数法
先把这几个数的质因数写出来,最小公倍数等于它们所有的质因数的乘积。
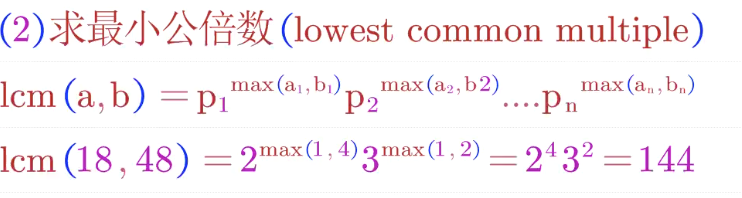
4.2 公式法
由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。即(a,b)×[a,b]=a×b。
